Recherches dans un tableau

Rechercher une valeur

Considérons le tableau suivant : nombres = [8, 7, 2, 10, 3, 1, 6, 5, 9, 4] et cherchons-y la valeur 5.

Contrairement à nous, l'ordinateur n'a pas une vue d'ensemble des valeurs, il ne peut pas immédiatement « voir » le 5 vers la fin du tableau.

Son approche est plus rudimentaire : il passe en revue tous les éléments du tableau jusqu'à trouver le 5 :

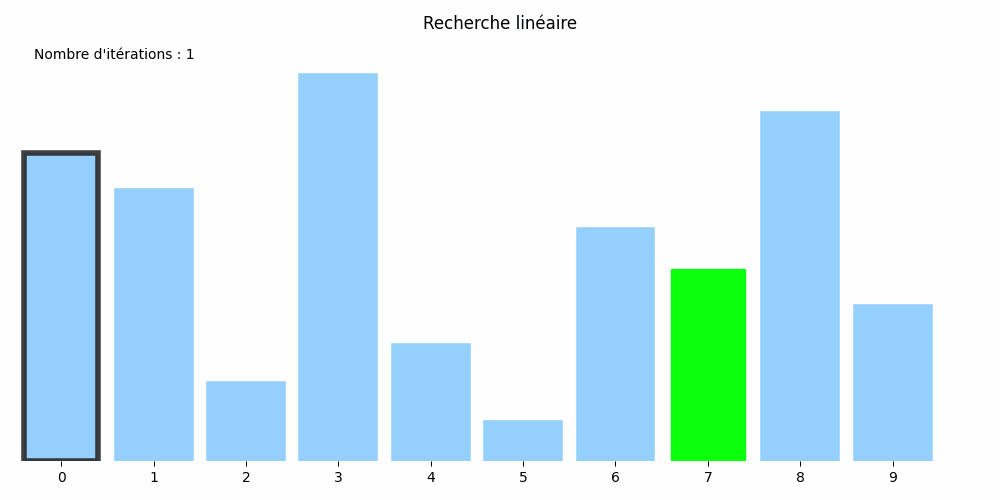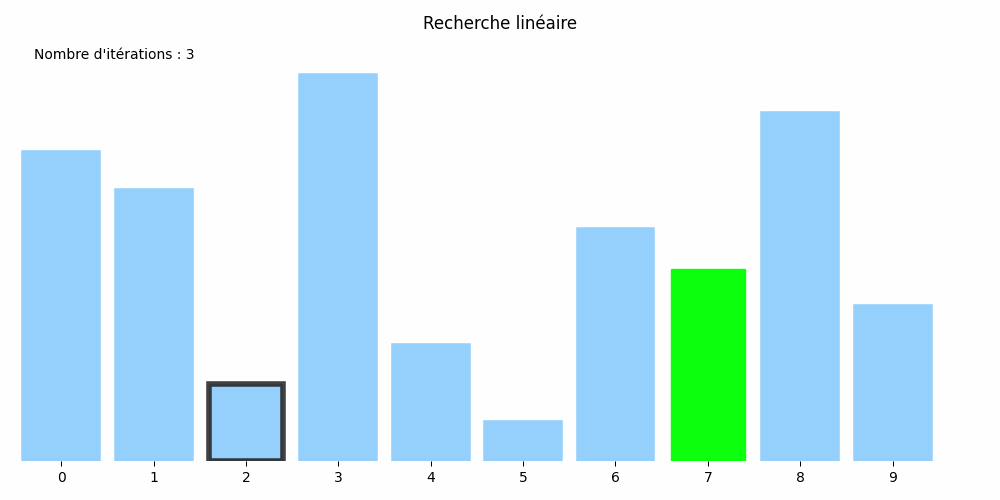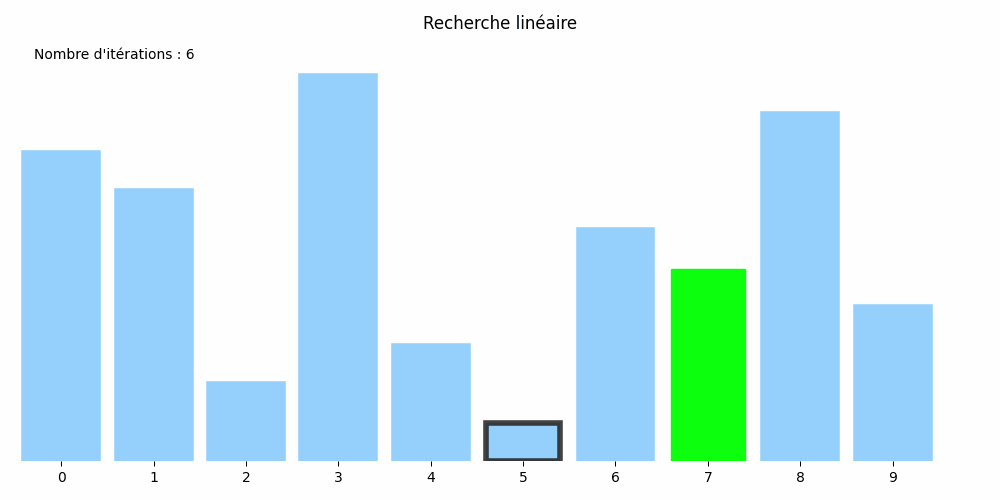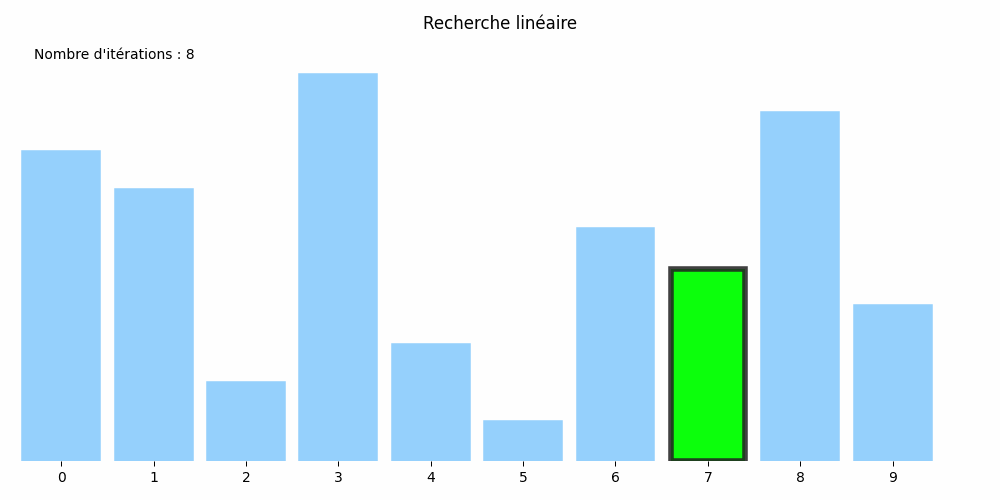
Cette méthode est appelée la recherche linéaire ou méthode par balayage.

La fonction lineaire

Compléter la fonction lineaire prenant en argument un tableau et une valeur x et renvoyant l'indice de la première occurrence de x dans tableau.

Si x n'est pas présent dans tableau, la fonction renverra None

###

LancerTéléchargerTéléverser RechargerSauvegarder

def lineaire(tableau, x):bksl-nl ...bksl-nlbksl-nlbksl-nltableau = [8, 7, 2, 10, 3, 1, 6, 5, 9, 5, 4]bksl-nlassert lineaire(tableau, 5) == 7, "Erreur en cherchant 5"bksl-nlassert lineaire(tableau, 0) is None, "Erreur en cherchant 0"bksl-nlprint("Bravo !")bksl-nlbksl-nl

Solution

🐍 Script Python

def lineaire(tableau, x):
    for i in range(len(tableau)):
        if tableau[i] == x:
            return i
    return None

En réalité, le return None de la dernière ligne n'est pas nécessaire car en Python une fonction renvoie None par défaut .

Étudions en détails le déroulement de cette fonction en comptant le nombre d'opérations:

• l'algorithme est construit autour d'une boucle « Pour »,
• à chaque itération, la variable i se voit affecter une nouvelle valeur : \(1\) affectation,
• on teste ensuite si tableau[i] est égal à x : \(1\) accès à la valeur de tableau[i] et \(1\) comparaison,
• s'il y a égalité on renvoie i : \(1\) retour,
• en fin de boucle on renvoie None : \(1\) retour.

Remarque

Ce décompte du nombre d'opérations est simpliste. En réalité, Python exécute plus d'opérations.

Si l'on fait le total, on se rend compte que chaque tour de boucle (sans tenir compte du return) nécessite \(3\) opérations. Le return quant à lui, qu'il renvoie un indice ou None rajoute \(1\) opération à l'ensemble.

Dans l'exemple précédent, le 5 cherché était à l'indice 7. Il a donc fallu \(8\) itérations et \(3\times 8 +1=25\) opérations au total.

Compter les opérations ou les itérations

On considère toujours le tableau nombres = [8, 7, 2, 10, 3, 1, 6, 5, 9, 4] et l'on effectue des recherches linéaires.

Cocher la ou les affirmations correctesSolution

• La recherche de 8 nécessite une seule itération
• La recherche de 8 nécessite une seule opération
• La recherche de 6 nécessite \(19\) opérations
• La recherche de 4 nécessite \(31\) opérations

• 8 est à l'indice 0. Il faut donc bien une seule itération
• Non car chaque itération nécessite à elle seule \(3\) opérations
• 6 est à l'indice 6. Il faut donc \(7\) itérations et \(3\times 7 + 1= 22\) opérations
• 4 est à l'indice 9. Il faut donc \(10\) itérations et bien \(3\times 10 + 1= 31\) opérations

Le décompte précis des opérations peut être laborieux et très sensible au langage de programmation ou aux instructions saisies pour mettre en œuvre l'algorithme.

Important

Nous allons donc désormais nous contenter de compter les itérations qui ne font que des opérations élémentaires.

Compter les itérations

On a modifié la fonction lineaire afin qu'elle renvoie le nombre d'itérations nécessaires effectuées lors de la recherche de x dans tableau. Cette nouvelle fonction s'appelle lineaire_bis

Si vous exécutez ce code, vous retrouverez le résultat précédent : rechercher 5 nécessite \(8\) itérations.

Modifier x et tableau (si besoin) afin que la recherche de x dans tableau nécessite :

• 1 itération
• 2 itérations
• 5 itérations dans un tableau de 5 valeurs
• 5 itérations dans un tableau de 6 valeurs
• 5 itérations dans un tableau contenant 2 fois la valeur cherchée
• 6 itérations dans un tableau de 6 valeurs sans que x ne soit présent dans tableau

###

LancerTéléchargerTéléverser RechargerSauvegarder

#--- HDR ---#bksl-nldef lineairepy-undbis(tableau, x):bksl-nl nbpy-unditerations = 0bksl-nl for i in range(len(tableau)):bksl-nl nbpy-unditerations += 1bksl-nl if tableau[i] == x:bksl-nl return ibksl-nl return nbpy-unditerationsbksl-nl#--- HDR ---#bksl-nl# À modifierbksl-nltableau = [8, 7, 2, 10, 3, 1, 6, 5, 9, 5, 4]bksl-nlx = 5bksl-nlbksl-nlnbpy-unditérations = lineairepy-undbis(tableau, x)bksl-nlprint(f"Il y a eu {nbpy-unditérations} itération(s).")bksl-nlbksl-nl

Solution

• 1 itération : Par exemple lineaire([0], 0)

• 2 itérations : Par exemple lineaire([0, 1], 2)

• 5 itérations dans un tableau de 5 valeurs : Par exemple lineaire([1, 2, 3, 4, 5], 5)
• 5 itérations dans un tableau de 6 valeurs : Par exemple lineaire([1, 2, 3, 4, 5, 6], 5)
• 5 itérations dans un tableau contenant 2 fois la valeur cherchée : Par exemple lineaire([1, 2, 3, 4, 5, 5], 5)
• 6 itérations dans un tableau de 6 valeurs sans que x ne soit présent dans tableau : Par exemple lineaire([1, 2, 3, 4, 5, 6], 7)

On l'a deviné, l'algorithme effectue un maximum d'itérations dans deux cas de figure :

• soit x est le dernier élément de tableau,
• soit x n'est pas présent dans tableau.

Ce sont les deux pires des cas.

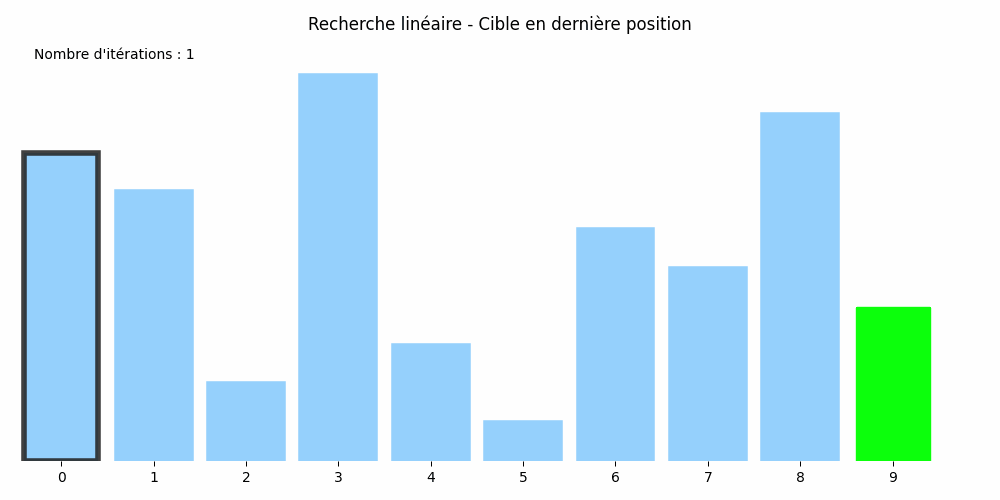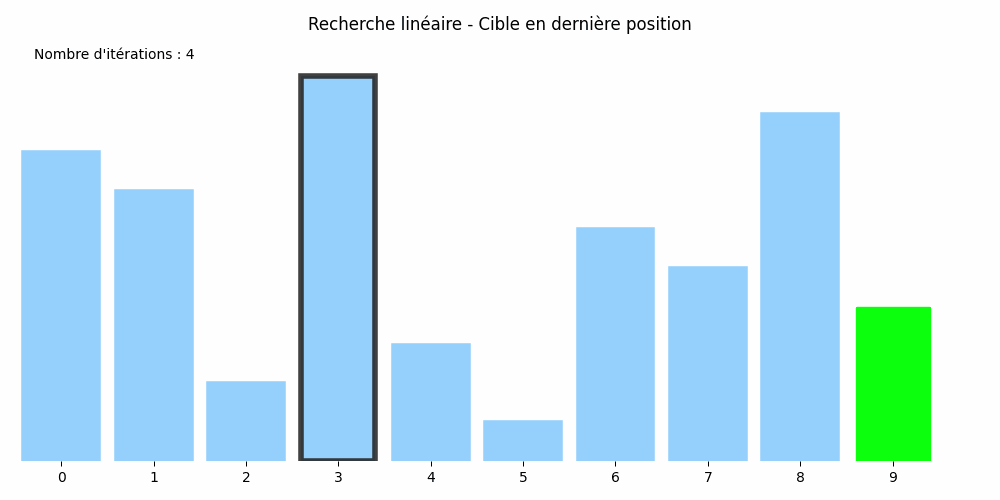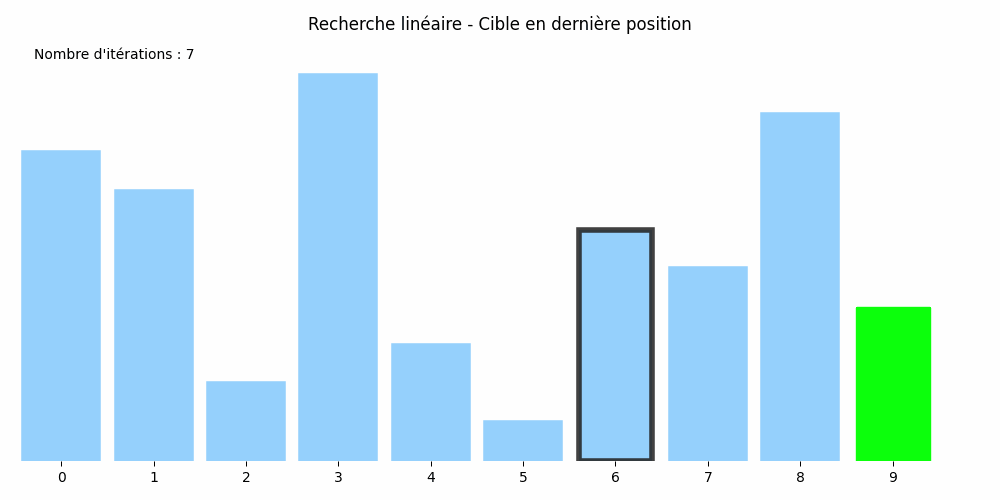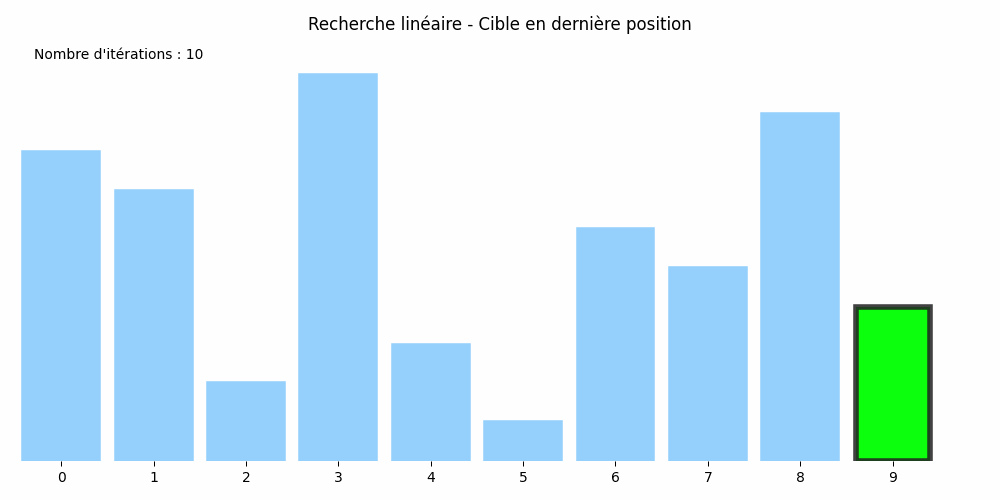
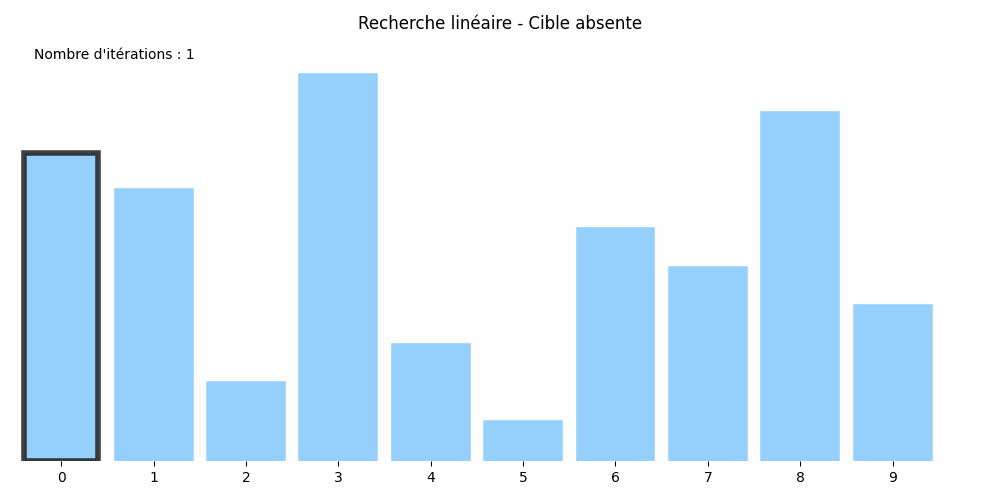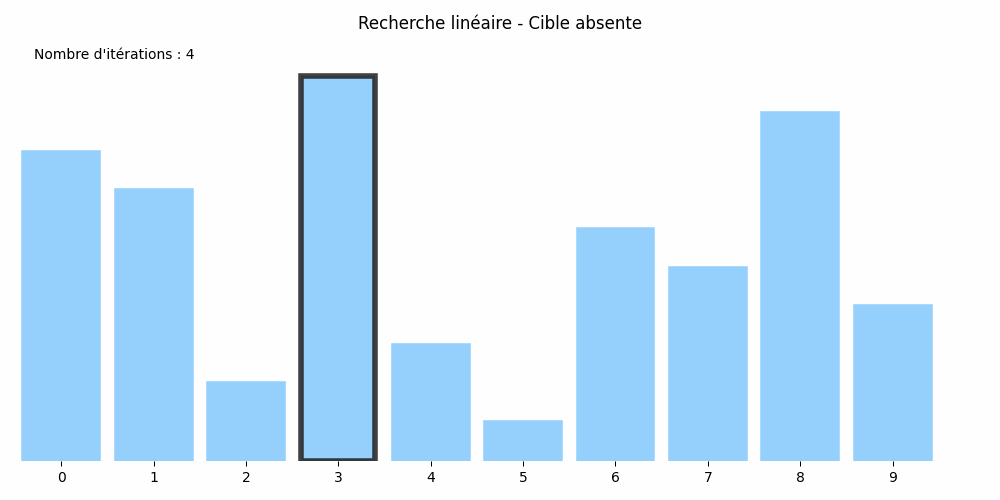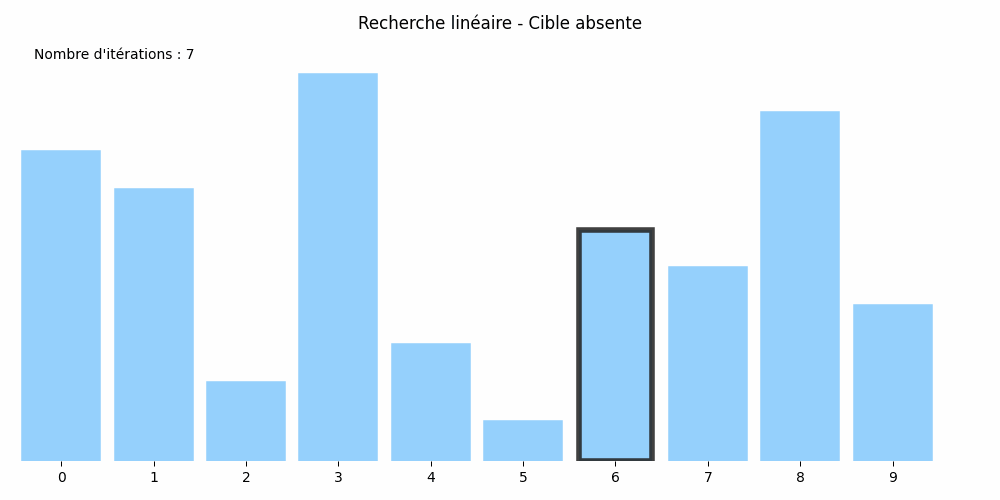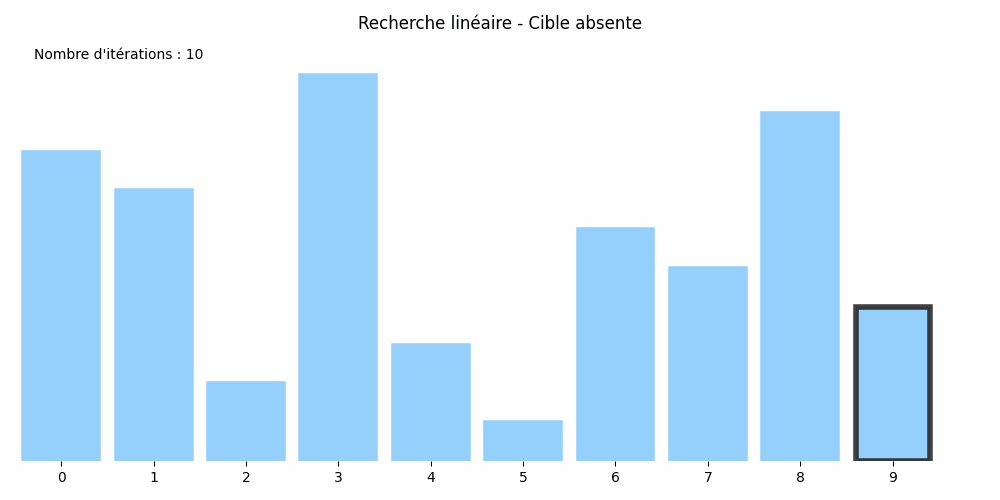
Dans chacun d'eux, si le tableau compte \(N\) éléments, il y aura \(N\) itérations. Le nombre d'itérations est égal à la taille du tableau. On dit que l'algorithme de recherche linéaire est de coût linéaire.

Rechercher le minimum

Le tri par sélection nécessite de trouver la valeur minimale du tableau afin de la placer en première position. Ceci fait on recommence à partir de la deuxième position, puis de la troisième, etc.

Nous nous intéressons dans cette partie à la recherche du minimum.

Rechercher le minimum

Cocher la ou les affirmations correctesSolution

• Dans le tableau \([3,\,8,\,7,\,1,\,2]\) la recherche du minimum nécessite \(4\) itérations
• Dans le tableau \([1,\,2,\,3,\,4]\) la recherche du minimum nécessite \(4\) itérations
• La recherche du minimum est plus courte s'il est placé au début du tableau
• Dans le tableau \([8,\,8,\,8,\,8]\) la recherche du minimum nécessite \(1\) itération

• Dans le tableau \([3,\,8,\,7,\,1,\,2]\) la recherche du minimum nécessite \(4\) itérations
• Dans le tableau \([1,\,2,\,3,\,4]\) la recherche du minimum nécessite \(4\) itérations
• La recherche du minimum est plus courte s'il est placé au début du tableau
• Dans le tableau \([8,\,8,\,8,\,8]\) la recherche du minimum nécessite \(1\) itération

Il faut lire l'ensemble des valeurs une fois pour être sûr de bien déterminer le minimum. Donc pour un tableau de taille \(N\), il faut faire \(N\) itérations.

On l'a compris, la recherche du minimum nécessite de lire toutes les valeurs une seule fois : le coût est donc linéaire (proportionnel à la taille du tableau).

La fonction minimum

Compléter la fonction minimum prenant en argument un tableau et renvoyant l'indice de la première occurrence du minimum dans tableau.

On garantit que tableau est non vide.

###

LancerTéléchargerTéléverser RechargerSauvegarder

def minimum(tableau):bksl-nl ...bksl-nlbksl-nlbksl-nlassert minimum([3, 8, 5]) == 0, "Erreur avec [3, 8, 5]"bksl-nlassert minimum([8, 5]) == 1, "Erreur avec [8, 5]"bksl-nlassert minimum([8]) == 0, "Erreur avec [8]"bksl-nlprint("Bravo !")bksl-nlbksl-nl

Solution

🐍 Script Python

def minimum(tableau):
    i_mini = 0
    for i in range(1, len(tableau)):
        if tableau[i] < tableau[i_mini]:
            i_mini = i
    return i_mini