Tri fusion

Mentionné dans le programme de Terminale

Le tri fusion n'est mentionné que dans le programme de Terminale NSI.

Sa mise en œuvre fait de plus appel à la notion de récursivité, notion abordée seulement en classe de Terminale.

Le tri fusion en bref

On partage le tableau en deux « moitiés » gauche et droite et on trie récursivement ces moitiés. On réalise ensuite la fusion de ces deux parties.

Algorithme

Quels sont les tableaux les plus simples à trier ? On pourrait répondre les tableaux d'ores et déjà triés dans l'ordre croissant mais encore faudrait-il s'assurer qu'ils sont triés.

La réponse est plus simple : les tableaux les plus simples à trier sont les tableaux de longueur \(1\) ou \(0\). En effet, un tableau ne contenant qu'une valeur est toujours trié !

Deuxième question : si l'on se donne deux tableaux (dont un au moins est non vide) triés dans l'ordre croissant et que l'on demande de les fusionner afin de créer un nouveau tableau trié, comment trouver le plus petit élément du nouveau tableau ?

Fusion de deux tableaux

On se donne deux tableaux (dont un au moins est non vide) l'un et l'autre triés dans l'ordre croissant et on cherche à créer un nouveau tableau comprenant les mêmes éléments triés dans l'ordre croissant.

Où se trouve le minimum du nouveau tableau ?

Cocher la ou les affirmations correctesSolution

• Au début du premier tableau
• Au début du second tableau
• Au début du premier ou du second tableau
• À la fin du premier ou du second tableau

• Au début du premier tableau
• Au début du second tableau
• Au début du premier ou du second tableau
• À la fin du premier ou du second tableau

Le minimum du nouveau tableau est le minimum de l'un des deux tableaux de départ. Il est donc situé en première position de l'un des deux tableaux initiaux. Il est impossible a priori de savoir si ce minimum sera dans le premier ou le second tableau.

Observons la fusion de deux tableaux de deux éléments :

État initialAprès une étapeAprès deux étapesAprès trois étapesAprès quatre étapes

Les tableaux de gauche et de droite initiaux sont triés.

Le nouveau minimum est le plus petit élément dans les tableaux de gauche et de droite.

Le nouveau minimum est le plus petit élément restant dans les tableaux de gauche et de droite.

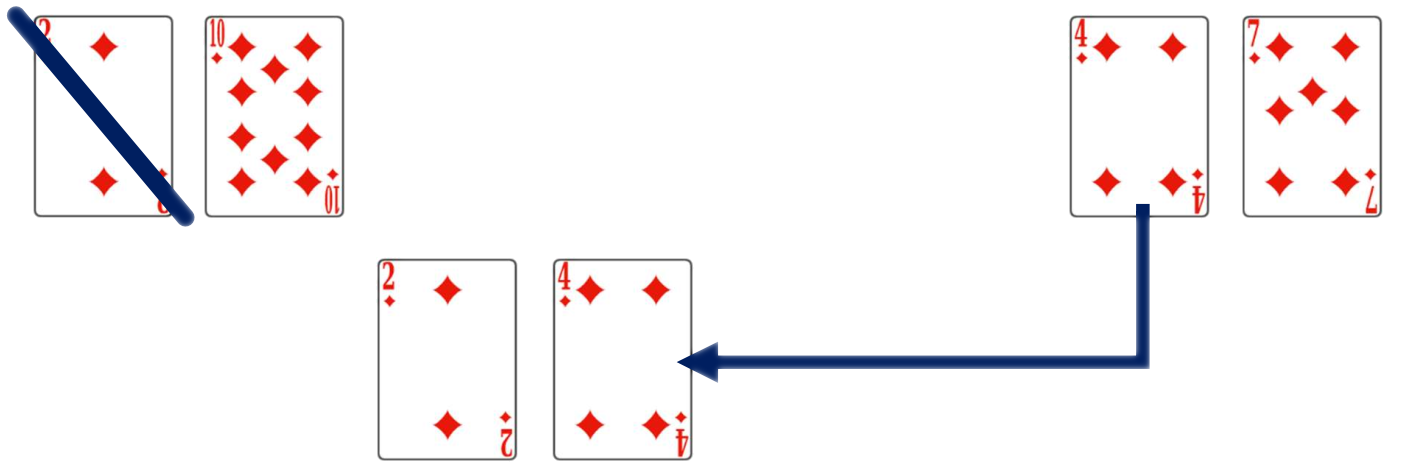
Le nouveau minimum est le plus petit élément restant dans les tableaux de gauche et de droite.

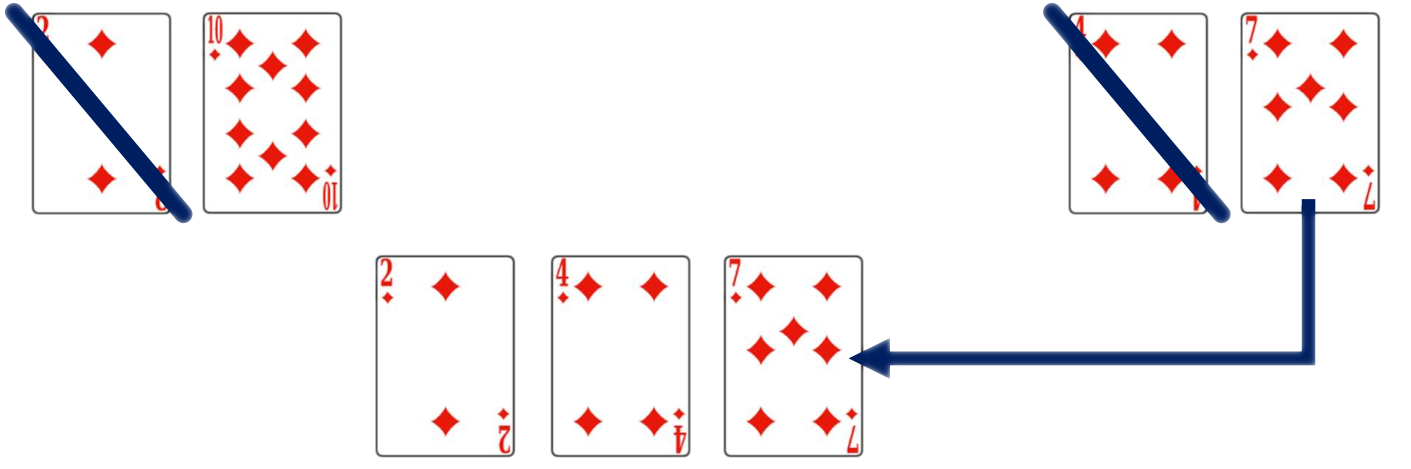
Le tableau de droite est vide : on pioche nécessairement dans le tableau de gauche.

---

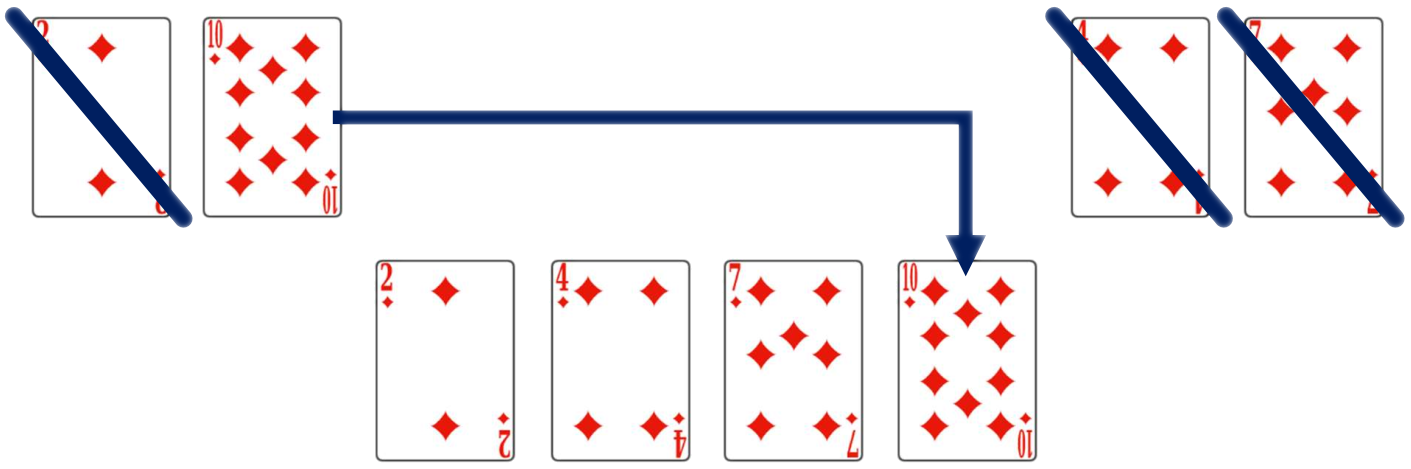
Ces deux observations (un tableau de longueur \(1\) est toujours trié ; il est simple de fusionner deux tableaux triés) permettent de construire l'algorithme de tri fusion. Il utilise la méthode « Diviser Pour Régner ».

Diviser pour régner

Contrairement à ce que son nom laisse penser, cette méthode de résolution de problèmes repose sur trois étapes :

• « Diviser » : partager un problème de grande taille en différents problèmes plus petits. On répète ces partages jusqu'à obtenir des problèmes faciles à résoudre,
• « Régner » : résoudre ces petits problèmes,
• « Combiner » : combiner les solutions des problèmes intermédiaires afin de construire la solution du problème initial.

Dans le cas présent, les trois étapes sont :

• « Diviser » : partager le tableau en deux moitiés gauche et droite. Ce partage en deux moitiés est répété récursivement jusqu'à obtenir des tableaux de taille \(0\) ou \(1\) ;
• « Régner » : trier les tableaux de taille \(0\) ou \(1\)... C'est immédiat car ils sont déjà triés !
• « Combiner » : fusionner les tableaux triés de proche en proche jusqu'à reconstituer le tableau initial... trié !

Tableau aléatoire Tableau croissant Tableau décroissant

Trier votre tableau

Coût du tri fusion

Le coût de cet algorithme n'est pas évident à déterminer.

Il faut tout d'abord déterminer le nombre d'étapes de partage nécessaires. Par exemple pour un tableau de taille \(8\) :

    graph LR
    A[Tableau de 8 éléments]
    subgraph "Partages (1)"
    B[4 éléments]
    C[4 éléments]
    end
    subgraph "Partages (2)"
    D[2 éléments]
    E[2 éléments]
    F[2 éléments]
    G[2 éléments]
    end
    subgraph "Partages (3)"
    H[1 élément]
    I[1 élément]
    J[1 élément]
    K[1 élément]
    L[1 élément]
    M[1 élément]
    N[1 élément]
    O[1 élément]
    end
    A --> B
    A --> C
    B --> D
    B --> E
    C --> F
    C --> G
    D --> H
    D --> I
    E --> J
    E --> K
    F --> L
    F --> M
    G --> N
    G --> O

Comme on peut le voir sur la figure, pour un tableau de \(8\) éléments il faut \(3\) étapes de partage.

Combien d'étapes de partage ?

Dans les propositions ci-dessous, \(N\) est la taille du tableau.

Cocher la ou les affirmations correctesSolution

• Si \(N=4\), il faut \(2\) étapes de partage
• Si \(N=5\), il faut \(2\) étapes de partage
• Si \(N=9\), il faut \(3\) étapes de partage
• Si \(N=256\), il faut \(8\) étapes de partage

• La première étape de partage crée deux tableaux de taille \(2\) que l'on partage en \(4\) tableaux de taille \(1\)
• La première étape de partage crée un tableau de \(2\) éléments et un autre de \(3\) éléments. Le second tableau doit être partagé encore deux fois avant d'atteindre la taille \(1\). Il faut donc \(3\) étapes de partage
• Il faut \(4\) étapes de partage. En effet, \(9 = 5 + 4 = (3 + 2) + (2 + 2)\) et le tableau de longueur \(3\) nécessite encore \(2\) partages
• \(256 = 2^8\) donc il faut bien \(8\) étapes de partage

On le comprend, le nombre d'étapes de partage est lié au nombre de quotients par \(2\) nécessaires pour passer de la longueur \(N\) à \(1\) ou \(0\).

Par exemple avec un tableau de \(25\) éléments :

• \(25\) ➞ \(12\) et \(13\) ;
• \(13\) ➞ \(6\) et \(7\) ;
• \(7\) ➞ \(3\) et \(4\) ;
• \(4\) ➞ \(2\) et \(2\) ;
• \(2\) ➞ \(1\) et \(1\).

Il faut donc \(5\) étapes de partage. On peut remarquer que \(2^4 < 25 \le 2^5\).

Les partages étant effectués, il faut trier les tableaux de longueur \(0\) ou \(1\) (immédiat) et les fusionner.

En partant de \(8\) éléments, on obtient \(8\) tableaux de longueur \(1\). On fusionne ces tableaux deux par deux. Cette étape nécessite de recopier l'ensemble des \(8\) valeurs dans les tableaux fusionnés.

On obtient alors \(4\) tableaux de longueur \(2\). Leur fusion par paires nécessite \(2\) copies de \(4\) valeurs. Là encore \(8\) opérations.

Enfin, on fusionne les \(2\) tableaux de \(4\) éléments : \(8\) opérations sont nécessaires.

On peut remarquer qu'il y a eu \(3\) étapes de fusions, tout comme il y avait eu \(3\) étapes de partage.

    graph LR
    H[Tableau de 1 élément]
    I[Tableau de 1 élément]
    J[Tableau de 1 élément]
    K[Tableau de 1 élément]
    L[Tableau de 1 élément]
    M[Tableau de 1 élément]
    N[Tableau de 1 élément]
    O[Tableau de 1 élément]
    subgraph "4 × 2 = 8"
    D[2 éléments]
    E[2 éléments]
    F[2 éléments]
    G[2 éléments]
    end
    subgraph "2 × 4 = 8"
    B[4 éléments]
    C[4 éléments]
    end
    subgraph "1 × 8 = 8"
    A[8 éléments]
    end
    H ---> D
    I ---> D
    J ---> E
    K ---> E
    L ---> F
    M ---> F
    N ---> G
    O ---> G
    D ---> B
    E ---> B
    F ---> C
    G ---> C
    B ---> A
    C ---> A

Résumons :

• le nombre d'étapes de partage est égal au nombre de fois où il est possible de diviser \(N\) par \(2\),
• les fusions nécessitent de recopier l'ensemble des \(N\) valeurs. Il y a autant d'étapes de fusions que d'étapes de partage.

Remarque

Le nombre d'étapes de partage peut être mis en rapport avec le nombre de bits constituant l'écriture binaire de la taille du tableau initial.

Ainsi, \(25\) s'écrit \(11001\) en binaire, sur \(5\) bits donc. On retrouve les \(5\) étapes de partage mentionnées plus haut.

Le nombre d'étapes de partage peut donc être exprimé à l'aide du logarithme en base 2 de la taille du tableau initial.

Diviser

Trier un tableau à l'aide du tri fusion nécessite donc de le partager en deux sous-tableaux de mêmes longueurs (à un élément près dans le cas où la taille est impaire).

Nous allons écrire une fonction effectuant cette tâche.

La fonction sous_tableau

Compléter la fonction sous_tableau prenant en argument un tableau ainsi que deux entiers debut et fin et renvoyant un nouveau tableau reprenant les éléments de tableau situés entre les indices debut (inclus) et fin (exclu).

###

LancerTéléchargerTéléverser RechargerSauvegarder

def souspy-undtableau(tableau, debut, fin):bksl-nl """bksl-nl Renvoie une copie des éléments d'indicesbksl-nl compris entre debut (inclus) et fin (exclu)bksl-nl de tableaubksl-nl """bksl-nl nouveau = [None] py-str (fin - debut) # pas indispensablebksl-nl ...bksl-nlbksl-nlbksl-nltableau = [8, 9, 10, 11, 12, 13]bksl-nlbksl-nl# Testsbksl-nlassert souspy-undtableau(tableau, 0, 2) == [8, 9]bksl-nlassert souspy-undtableau(tableau, 2, 6) == [10, 11, 12, 13]bksl-nlassert souspy-undtableau(tableau, 0, 6) == [8, 9, 10, 11, 12, 13]bksl-nlassert souspy-undtableau(tableau, 0, 0) == []bksl-nlprint("Bravo !")bksl-nlbksl-nl

Solution

🐍 Script Python

def sous_tableau(tableau, debut, fin):
    """
    Renvoie une copie des éléments d'indices
    compris entre debut (inclus) et fin (exclu)
    de tableau
    """
    nouveau = [None] * (fin - debut)
    for i in range(debut, fin):
        nouveau[i - debut] = tableau[i]
    return nouveau

On préférera néanmoins une version plus concise de cette fonction qui utilise les listes par compréhension :

🐍 Script Python

def sous_tableau(tableau, debut, fin):
    """
    Renvoie une copie des éléments d'indices
    compris entre debut (inclus) et fin (exclu)
    de tableau
    """
    return [tableau[valeur] for valeur in range(debut, fin)]

Enfin, Python offre la possibilité d'extraire des sous-tableaux à l'aide des copies de tranches : tableau[a:b] renvoie ainsi une nouvelle liste constituée des éléments d'indices a (inclus) à b (exclu) de tableau.

La fonction précédente peut donc aussi s'écrire :

🐍 Script Python

def sous_tableau(tableau, debut, fin):
    """
    Renvoie une copie des éléments d'indices
    compris entre debut (inclus) et fin (exclu)
    de tableau
    """
    return tableau[debut:fin]

Utilisation

Il sera donc possible de récupérer les moitiés gauche et droite du tableau en faisant :

🐍 Script Python

milieu = len(tableau) // 2
gauche = sous_tableau(tableau, 0, milieu)
droite = sous_tableau(tableau, milieu, len(tableau))

Lien avec le coût

Ces différentes copies des sous-tableaux (ou du tableau initial dans d'autres versions du tri fusion) ont un coût : il faut recopier les valeurs (coût en temps) et aussi les stocker (coût en espace).

De plus l'accès à ces valeurs copiées est souvent plus lent (elles peuvent ne pas être stockées dans la mémoire cache du processeur) ce qui ralentit l'exécution du tri fusion.

Fusionner

On l'a compris, le partage du tableau se fait autant de fois que nécessaire jusqu'à obtenir des sous-tableaux contenant 0 ou 1 élément. Ces sous-tableaux sont déjà triés.

Il reste donc à les fusionner.

La fonction fusion

On demande d'écrire une fonction fusion prenant en argument deux tableaux gauche et droite et renvoyant le tableau obtenu en les fusionnant.

On précise que :

• les deux tableaux gauche et droite sont triés dans l'ordre croissant,
• ils n'ont pas obligatoirement la même longueur,
• le tableau renvoyé doit contenir toutes les valeurs des tableaux initiaux et doit lui aussi être trié dans l'ordre croissant.

La démarche proposée consiste à :

• créer un tableau contenant autant de valeurs que nécessaire,

• créer trois indices permettant de savoir où l'on doit écrire dans le nouveau tableau et où l'on doit lire dans les tableaux gauche et droite,

• lire le premier élément de chacun des deux tableaux d'entrée et recopier le plus petit des deux au début du nouveau tableau,

• mettre à jour les indices en conséquence,

• recommencer jusqu'à avoir lu la totalité de l'un des deux tableaux de départ,

• recopier la fin de l'autre tableau dans le nouveau tableau.

###

LancerTéléchargerTéléverser RechargerSauvegarder

def fusion(gauche, droite):bksl-nl """bksl-nl Fusionne gauche et droitebksl-nl Les tableaux intiaux sont triésbksl-nl Le tableau résultat l'est aussibksl-nl """bksl-nl taillepy-undgauche = len(gauche)bksl-nl taillepy-unddroite = len(droite)bksl-nl nouveau = [None] py-str (... + ...)bksl-nlbksl-nl ipy-undnouveau = 0bksl-nl ipy-undgauche = 0bksl-nl ipy-unddroite = 0bksl-nlbksl-nl # Il reste des éléments à gauche ET à droitebksl-nl while ipy-undgauche < ... and ... < taillepy-unddroite:bksl-nl if gauche[...] <= droite[...]:bksl-nl nouveau[ipy-undnouveau] = gauche[...]bksl-nl ipy-undgauche += 1bksl-nl else:bksl-nl nouveau[...] = ...[...]bksl-nl ...bksl-nl ipy-undnouveau += 1bksl-nlbksl-nl # Il ne reste des éléments QUE à gauchebksl-nl while ipy-undgauche < ...:bksl-nl nouveau[...] = gauche[...]bksl-nl ipy-undgauche += 1bksl-nl ipy-undnouveau += 1bksl-nlbksl-nl # Il ne reste des éléments QUE à droitebksl-nl while ...:bksl-nl ...bksl-nl ...bksl-nl ...bksl-nlbksl-nl return ...bksl-nlbksl-nlbksl-nl# Même taillebksl-nlgauche = [0, 2, 4]bksl-nldroite = [1, 3, 5]bksl-nlassert fusion(gauche, droite) == [0, 1, 2, 3, 4, 5], "Erreur avec gauche = [0, 2, 4] et droite = [1, 3, 5]"bksl-nl# Un tableau plus courtbksl-nlgauche = [0, 2, 4]bksl-nldroite = [1, 3]bksl-nlassert fusion(gauche, droite) == [0, 1, 2, 3, 4], "Erreur avec gauche = [0, 2, 4] et droite = [1, 3]"bksl-nl# Un tableau videbksl-nlgauche = []bksl-nldroite = [1, 3, 5]bksl-nlassert fusion(gauche, droite) == [1, 3, 5], "Erreur avec gauche = [] et droite = [1, 3, 5]"bksl-nl# gauche est toujours plus petitbksl-nlgauche = [0, 1]bksl-nldroite = [2, 3]bksl-nlassert fusion(gauche, droite) == [0, 1, 2, 3], "Erreur avec gauche = [0, 1] et droite = [2, 3]"bksl-nlbksl-nlbksl-nlprint("Bravo !")bksl-nlbksl-nl

Solution

🐍 Script Python

def fusion(gauche, droite):
    """
    Fusionne gauche et droite
    Les tableaux initiaux sont triés
    Le tableau résultat l'est aussi
    """
    taille_gauche = len(gauche)
    taille_droite = len(droite)
    nouveau = [None] * (taille_gauche + taille_droite)

    i_nouveau = 0
    i_gauche = 0
    i_droite = 0

    # Il reste des éléments à gauche ET à droite
    while i_gauche < taille_gauche and i_droite < taille_droite:
        if gauche[i_gauche] <= droite[i_droite]:
            nouveau[i_nouveau] = gauche[i_gauche]
            i_gauche += 1
        else:
            nouveau[i_nouveau] = droite[i_droite]
            i_droite += 1
        i_nouveau += 1

    # Il ne reste des éléments QUE à gauche
    while i_gauche < taille_gauche:
        nouveau[i_nouveau] = gauche[i_gauche]
        i_gauche += 1
        i_nouveau += 1

    # Il ne reste des éléments QUE à droite
    while i_droite < taille_droite:
        nouveau[i_nouveau] = droite[i_droite]
        i_droite += 1
        i_nouveau += 1

    return nouveau

Solution alternative

L'approche précédente est classique. Il est néanmoins possible de la réécrire à l'aide d'une unique boucle bornée (au lieu de trois boucles non bornées).

🐍 Script Python

def fusion(gauche, droite):
    """
    Fusionne gauche et droite
    Les tableaux initiaux sont triés
    Le tableau résultat l'est aussi
    """
    taille_gauche = len(gauche)
    taille_droite = len(droite)
    nouveau = [None] * (taille_gauche + taille_droite)

    i_nouveau = 0
    i_gauche = 0
    i_droite = 0

    for i_nouveau in range(taille_gauche + taille_droite):
        if i_gauche < taille_gauche and (i_droite >= taille_droite or gauche[i_gauche] <= droite[i_droite]):
            nouveau[i_nouveau] = gauche[i_gauche]
            i_gauche += 1
        else:
            nouveau[i_nouveau] = droite[i_droite]
            i_droite += 1

    return nouveau

En entier

Il reste à écrire la fonction de tri.

Contrairement aux tris par insertion et sélection étudiés précédemment, on choisit ici d'écrire une version renvoyant un nouveau tableau trié. Cette version n'est donc pas en place.

Le pseudo-code de la fonction tri_fusion est donc le suivant :

📋 Pseudo-code

Fonction tri_fusion(tableau) :
    Si la taille de tableau est strictement inférieure à 2 :
        Renvoyer tableau

    milieu est l'indice du centre de tableau

    gauche est le résultat du tri fusion de la première « moitié » de tableau (avant l'indice milieu -exclu-)
    droite est le résultat du tri fusion de la seconde « moitié » de tableau (après l'indice milieu -inclus-)

    Renvoyer la fusion de gauche et droite

La fonction tri_fusion

Compléter la fonction tri_fusion prenant en argument un tableau et renvoyant un nouveau tableau, trié dans l'ordre croissant et contenant les mêmes valeurs que le tableau initial.

On pourra utiliser les fonctions sous_tableau et fusion.

###

LancerTéléchargerTéléverser RechargerSauvegarder

def souspy-undtableau(tableau, debut, fin):bksl-nl """bksl-nl Renvoie une copie des éléments d'indicesbksl-nl compris entre debut (inclus) et fin (exclu)bksl-nl de tableaubksl-nl """bksl-nl return [tableau[valeur] for valeur in range(debut, fin)]bksl-nlbksl-nlbksl-nldef fusion(gauche, droite):bksl-nl """bksl-nl Fusionne gauche et droitebksl-nl Les tableaux initiaux sont triésbksl-nl Le tableau résultat l'est aussibksl-nl """bksl-nl taillepy-undgauche = len(gauche)bksl-nl taillepy-unddroite = len(droite)bksl-nl nouveau = [None] py-str (taillepy-undgauche + taillepy-unddroite)bksl-nlbksl-nl ipy-undnouveau = 0bksl-nl ipy-undgauche = 0bksl-nl ipy-unddroite = 0bksl-nlbksl-nl # Il reste des éléments à gauche ET à droitebksl-nl while ipy-undgauche < taillepy-undgauche and ipy-unddroite < taillepy-unddroite:bksl-nl if gauche[ipy-undgauche] <= droite[ipy-unddroite]:bksl-nl nouveau[ipy-undnouveau] = gauche[ipy-undgauche]bksl-nl ipy-undgauche += 1bksl-nl else:bksl-nl nouveau[ipy-undnouveau] = droite[ipy-unddroite]bksl-nl ipy-unddroite += 1bksl-nl ipy-undnouveau += 1bksl-nlbksl-nl # Il ne reste des éléments QUE à gauchebksl-nl while ipy-undgauche < taillepy-undgauche:bksl-nl nouveau[ipy-undnouveau] = gauche[ipy-undgauche]bksl-nl ipy-undgauche += 1bksl-nl ipy-undnouveau += 1bksl-nlbksl-nl # Il ne reste des éléments QUE à droitebksl-nl while ipy-unddroite < taillepy-unddroite:bksl-nl nouveau[ipy-undnouveau] = droite[ipy-unddroite]bksl-nl ipy-unddroite += 1bksl-nl ipy-undnouveau += 1bksl-nlbksl-nl return nouveaubksl-nlbksl-nlbksl-nldef tripy-undfusion(tableau):bksl-nl """bksl-nl Trie tableau à l'aide du tri fusionbksl-nl Renvoie un nouveau tableau triébksl-nl """bksl-nl ...bksl-nlbksl-nlbksl-nltableaupy-und0 = [3, 1, 2]bksl-nlassert tripy-undfusion(tableaupy-und0) == [1, 2, 3], "Erreur avec [3, 1, 2]"bksl-nlbksl-nltableaupy-und1 = [1, 2, 3, 4]bksl-nlassert tripy-undfusion(tableaupy-und1) == [1, 2, 3, 4], "Erreur avec [1, 2, 3, 4]"bksl-nlbksl-nltableaupy-und2 = [-2, -5]bksl-nlassert tripy-undfusion(tableaupy-und2) == [-5, -2], "Erreur avec des valeurs négatives"bksl-nlbksl-nltableaupy-und3 = []bksl-nlassert tripy-undfusion(tableaupy-und3) == [], "Erreur avec un tableau vide"bksl-nlbksl-nltableaupy-und4 = [-7, 6, -8, 2, 9, 5, 10, 0]bksl-nlassert tripy-undfusion(tableaupy-und4) == [-8, -7, 0, 2, 5, 6, 9, 10], "Erreur avec [-7, 6, -8, 2, 9, 5, 10, 0]"bksl-nlbksl-nlprint("Bravo !")bksl-nlbksl-nl

Solution

🐍 Script Python

def tri_fusion(tableau):
    """
    Trie tableau à l'aide du tri fusion
    Renvoie un nouveau tableau trié
    """
    taille = len(tableau)
    # Cas de base, tableau de longueur 1 ou moins
    if taille < 2:
        return tableau

    milieu = taille // 2

    # Tris récursifs des parties gauche et droite
    gauche = tri_fusion(sous_tableau(tableau, 0, milieu))
    droite = tri_fusion(sous_tableau(tableau, milieu, taille))

    return fusion(gauche, droite)