Coût des boucles imbriquées⚓︎
Effectifs cumulés quadratiques⚓︎
On considère le tableau suivant donnant la répartition des notes lors d'une épreuve d'un concours :
resultats = [
5, 10, 2, 8, 9, 13, 11, 7, 8, 5,
13, 7, 11, 9, 15, 12, 17, 9, 10, 4, 0
]
Le 5 à l'indice 0 signifie que 5 candidats ont eu 0/20 à cette épreuve. Le 0 à l'indice 20 signifie qu'aucun candidat n'a eu 20/20.
On souhaite calculer les effectifs cumulés pour chaque note, c'est à dire, pour chaque note, calculer le nombre de candidats ayant eu cette note ou moins. Par exemple, 15 candidats ont eu 1/20 ou moins, 17 candidats ont eu 2/20 ou moins.
Une première approche naïve consiste à parcourir tous les effectifs et pour chacun à calculer la somme de ceux qui le précède.
La fonction sommes
Compléter la fonction sommes prenant en argument un tableau et renvoyant un nouveau tableau de même longueur contenant les valeurs cumulées du précédent.
Solution
On utilise une double boucle.
def sommes(tableau):
cumuls = [0] * len(tableau)
for i in range(len(tableau)):
for j in range(0, i + 1):
cumuls[i] += tableau[j]
return cumuls
Comme on le verra ci-dessous, cette version est inefficace.
Attardons-nous sur les sommes calculées dans le cas des résultats du concours :
- la première somme correspond aux candidats ayant eu 0/20 (ou moins ce qui n'est pas possible). Il y en a 5.
- la deuxième aux candidats ayant eu 1/20 ou moins. Il y en a 5 + 10 = 15.
- la troisième aux candidats ayant eu 2/20 ou moins. Il y en a 5 + 10 + 2 = 17.
- la quatrième aux candidats ayant eu 3/20 ou moins. Il y en a 5 + 10 + 2 + 8 = 25.
- ...
- la dernière aux candidats ayant eu 20/20 ou moins. Il y en a 5 + 10 + 2 + 8 + ... + 4 + 0 = 185.
Si l'on se concentre sur le décompte des nombres additionnés :
- il y en a \(1\) dans la première somme,
- il y en a \(2\) dans la deuxième somme,
- il y en a \(3\) dans la troisième somme,
- ...
- il y en a \(21\) dans la dernière somme.
Au total, cela fait donc \(1+2+3+...+21 = 231\) nombres additionnés.
De façon générale, si le tableau avait comporté \(N\) valeurs, il y aurait eu \(1+2+\dots+N\) nombres additionnés.
Combien vaut cette somme ? La figure ci-dessous nous donne une piste vers le résultat :
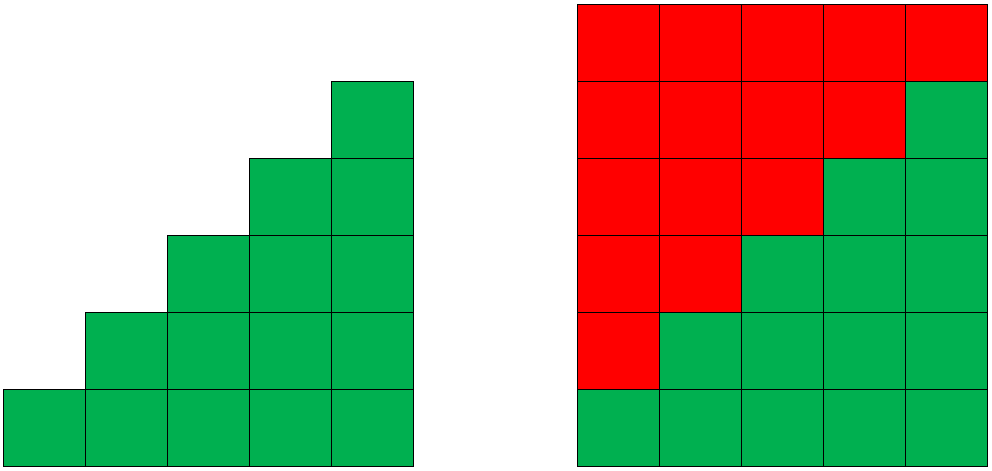
La somme \(1 + 2+...+5\) est représentée à gauche en vert. Calculer la valeur de cette somme revient à compter les carrés composant cette forme verte.
À droite on lui a ajouté la forme rouge qui représente la même somme \(1 + 2+...+5\)
Ces deux formes dessinent un rectangle de \(5\) carrés de large sur \(5+1=6\) de haut. Il compte donc \(5 \times 6\) carrés. La forme verte totalise donc \(\frac{5 \times 6}{2} = 15\) carrés.
De façon générale, on peut montrer que la somme \(1+2+...+N\) vaut \(\frac{N\times(N+1)}{2} = \frac12(N^2+N)\).
Pour de grand tableaux, le nombre de valeurs additionnées évolue principalement avec le carré de \(N\).
On dit que cet algorithme est de coût quadratique.
Le point important à retenir est que dans ce cas, si l'on double la taille des données, le nombre d'opérations va être multiplié par un facteur \(2^2 = 4\). Si on triple la taille des données, le facteur multiplicateur vaudra \(3^2=9\) !
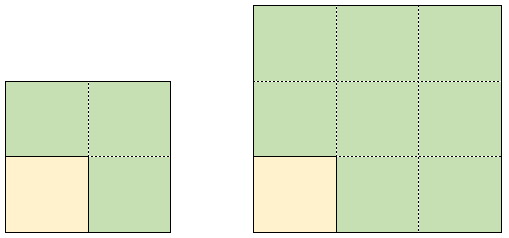
On peut rapprocher cette relation de celle liant la multiplication de la longueur d'un carré et l'évolution de son aire (figure ci-dessous).
Le coût quadratique
On considère un algorithme de coût quadratique. Pour une donnée d'entrée de taille \(N = 5\), l'algorithme a effectué \(30\) opérations.
- Pour une donnée d'entrée de taille \(N = 10\), l'algorithme effectuera environ \(60\) opérations
- Pour une donnée d'entrée de taille \(N = 10\), l'algorithme effectuera environ \(120\) opérations
- Pour une donnée d'entrée de taille \(N = 30\), l'algorithme effectuera plus de \(5\) opérations
- Pour une donnée d'entrée de taille \(N = 50\), l'algorithme effectuera environ \(3\,000\) opérations
Pour une donnée d'entrée de taille \(N = 10=2\times 5\), l'algorithme effectuera environ \(30\times2^2=120\) opérations
Pour une donnée d'entrée de taille \(N = 10\), l'algorithme effectuera environ \(120\) opérations
Pour une donnée d'entrée de taille \(N = 30=6\times 5\), l'algorithme effectuera plus de \(30\times 6^2=1\,080\) opérations
Pour une donnée d'entrée de taille \(N = 50\), l'algorithme effectuera environ \(3\,000\) opérations
Le coût est quadratique. Lorsque l'on multiplie la taille des entrées par \(k\), le nombre d'opérations est multiplié par \(k^2\).
Le coût quadratique (bis)
On considère un script Python mettant en œuvre un algorithme de coût quadratique.
L'exécution de ce script par un ordinateur pour une donnée d'entrée de taille \(N = 10\,000\) a mis \(0,3\) seconde.
On exécute à nouveau ce script sur le même ordinateur.
- Pour une donnée d'entrée de taille \(N = 20\,000\), le script s'exécute en \(0,6\) seconde
- Pour une donnée d'entrée de taille \(N = 100\,000\), le script s'exécute en \(3\) secondes
- Pour une donnée d'entrée de taille \(N = 1\,000\,000\), le script s'exécute en \(50\) minutes
- Pour une donnée d'entrée de taille \(N = 1\,000\), le script s'exécute en \(3\) millisecondes
On double la taille de l'entrée donc le temps d'exécution est multiplié par \(2^2=4\). Il faut donc \(0,3\times 4=1,2\) secondes
On multiplie la taille de l'entrée par \(10\) donc le temps d'exécution est multiplié par \(10^2=100\). Il faut donc \(0,3\times 100=30\) secondes
On multiplie la taille de l'entrée par \(100\) donc le temps d'exécution est multiplié par \(100^2=10\,000\). Il faut donc \(0,3\times 10\,000=3\,000\) secondes soit \(50\) minutes !
On divise la taille de l'entrée par \(10\) donc le temps d'exécution est divisé par \(10^2=100\). Il faut donc \(0,3 : 100=0,003\) secondes soit \(3\) millisecondes
Effectifs cumulés linéaires⚓︎
La méthode employée ci-dessus pour calculer les effectifs cumulés est coûteuse. Il est possible de calculer les mêmes valeurs en étant plus efficace.
En effet, pour les indices non nuls, l'effectif cumulé d'indice i est égal au précédent (indice i - 1) auquel on a simplement additionné la valeur d'indice i.
En procédant ainsi, on n'utilise chaque nombre qu'une seule fois : le coût est linéaire et est plus avantageux comme l'illustre la figure ci-dessous :
La fonction sommes_lineaires
Compléter la fonction sommes_lineaires prenant en argument un tableau et renvoyant un nouveau tableau de même longueur contenant les valeurs cumulées du précédent.
On utilisera une méthode de coût linéaire.
On garantit que tableau est non vide.
Solution
On utilise une simple boucle.
def sommes_lineaires(tableau):
cumuls = [0] * len(tableau)
cumuls[0] = tableau[0]
for i in range(1, len(tableau)):
cumuls[i] = cumuls[i - 1] + tableau[i]
return cumuls

