Sommet d'un tableau unimodal⚓︎
Un tableau unimodal est un tableau :
- comportant au moins trois éléments
- dont les premiers sont strictement croissants, jusqu'à un indice
i, - dont les éléments, à partir de
i, sont strictement décroissants.
Le sommet d'un tableau unimodal est sa plus grande valeur.
Ainsi :
[1, 2, 3, 2, 1, 0]est un tableau unimodal, son sommet est 3.[1, 2, 3, 5, 10, 9]est un tableau unimodal, son sommet est 10.[1, 2, 3]n'est pas un tableau unimodal, il n'y a pas de descente à la fin,[1, 2]non plus, il n'y a pas assez d'éléments (au moins trois),[5, 3, 0]non plus, il n'y a pas de montée au début.
Remarquons bien que le sommet n'est jamais la première valeur ni la dernière valeur.
Objectif⚓︎
Écrire une fonction utilisant le principe diviser pour régner afin de déterminer le sommet du tableau unimodal.
La fonction reçoit en paramètre un tableau intitulé valeurs, qu'on supposera unimodal, sous la forme d'une liste Python et renvoie son sommet.
L'emploi de la fonction max ou de tri est interdit dans ce sujet.
Ci-dessous une animation de la recherche du sommet avec les valeurs :
valeurs = [1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3]
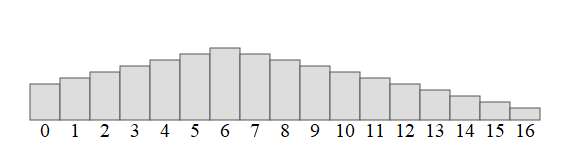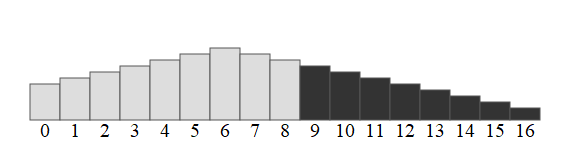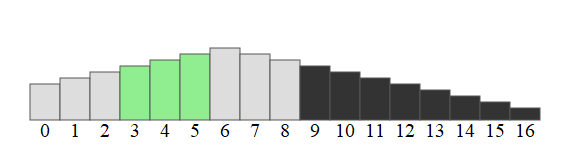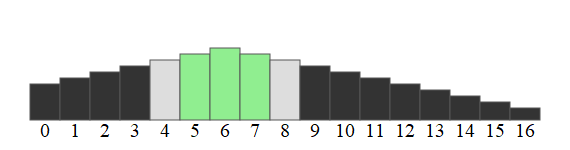
Principe de l'algorithme :
On cherche à déterminer l'indice de la valeur maximale.
C'est l'indice i_max tel que valeurs[i_max] > valeurs[i_max - 1] et valeurs[i_max] > valeurs[i_max + 1].
Pour cela on débute avec des indices gauche = 0 et droite = len(tableau) - 1 permettant de couvrir tout le tableau. On sait que gauche <= i_max <= droite.
À chaque étape, les variables gauche ou droite vont être modifiées.
On appelle l'indice milieu, l'indice central arrondi entre les indices gauche et droite.
On examine l'ordre dans lequel sont rangés les 3 éléments autour de celui d'indice milieu.
- Si ces éléments sont rangés par ordre croissant cela signifie que le sommet est situé à droite de celui d'indice
milieu. - Si ces éléments sont rangés par ordre décroissant cela signifie que le sommet est situé à gauche de celui d'indice
milieu. - Sinon, on a trouvé le sommet !
Algorithme naïf
Il est très simple de déterminer le sommet en parcourant de gauche à droite le tableau.
Notre objectif est de le faire avec un bien meilleur cout.
On rappelle que le tableau donné sera unimodal.
Exemples
>>> sommet([1, 2, 0])
2
>>> sommet([1, 9, 8, 7])
9
>>> sommet([1, 3, 5, 2])
5
>>> sommet([1, 2, 3, 4, 5, 4, 3, 2, 1])
5
>>> sommet([1, 2, 3, 4, 3, 2, 1, 0, -1, -2])
4
On complètera le code :
def sommet(tableau):bksl-nl gauche = 0bksl-nl droite = len(tableau) - 1bksl-nl while droite - gauche > 1:bksl-nl milieu = (...) // 2bksl-nl if tableau[milieu - 1] < tableau[milieu] < tableau[milieu + 1]:bksl-nl gauche = ...bksl-nl elif tableau[milieu - 1] > ... > ...:bksl-nl droite = ...bksl-nl else:bksl-nl return tableau[...]bksl-nlbksl-nlbksl-nl# testsbksl-nlassert sommet([1, 9, 8, 7]) == 9bksl-nlassert sommet([1, 3, 5, 2]) == 5bksl-nlassert sommet([1, 2, 3, 4, 5, 4, 3, 2, 1]) == 5bksl-nlassert sommet([1, 2, 3, 4, 3, 2, 1, 0, -1, -2]) == 4bksl-nlbksl-nldef sommet(tableau):bksl-nl gauche = 0bksl-nl droite = len(tableau) - 1bksl-nl while droite - gauche > 1:bksl-nl milieu = (gauche + droite) // 2bksl-nl if tableau[milieu - 1] < tableau[milieu] < tableau[milieu + 1]:bksl-nl gauche = milieubksl-nl elif tableau[milieu - 1] > tableau[milieu] > tableau[milieu + 1]:bksl-nl droite = milieubksl-nl else:bksl-nl return tableau[milieu]bksl-nlbksl-nl
A
Z